哪个开关? 脑筋急转弯
一栋建筑的底层有三个开/关开关。只有一个开关控制三楼的单个灯泡。其他两个开关未连接到任何东西。随意设置开关的开/关顺序。然后去三楼查看灯泡。不用离开三楼,你能弄清楚哪个开关是真的吗?你只有一次机会。
[答案:] 打开前两个开关,关闭第三个开关。等待 10 分钟,然后关闭第一个开关,去三楼。如果灯泡熄灭但发热,则第一个开关是控制它的开关;如果灯泡亮着,则第二个开关是真的;如果灯泡熄灭且发冷,则第三个开关是真的。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保未来能够继续讲述关于发现和塑造我们当今世界的想法的有影响力的故事。
[中断]

密码算术
在这些问题中,每个字母对应一个数字。例如,你能算出每个字母代表哪个数字才能使右侧的算式成立吗?
[答案:] S = 3 E = 0 V = 8 N = 7 F = 2 O = 1 R = 5 T = 6 Y = 4
要开始解决这个问题,请注意 7 乘以 N 等于某个以 9 结尾的数字,因此 N 必须是 7。从这个信息中,您就知道 7E + 4 等于某个以 Y 为个位数的数字,然后可以开始尝试。例如,E 不能是 1,因为那样 Y 也会是 1,如果 E 是 2,那么 V 就不能是 1。以这种方式继续推理最终会得出上面的答案。
[中断]
令人困惑的多面体
你能想象一个由正方形底面和四个等边三角形组成的实心金字塔,以及一个具有四个面与金字塔三角形面相同的实心四面体吗?现在将金字塔的一个三角形面粘合到四面体上的一个三角形上。由此产生的多面体有多少个面?不是七个!
[答案:] 在组合实体中,有两个位置两个三角形面——每个组成实体各一个——完美对齐,形成一个面。因此,新多面体的面总数仅为 5 个(一个正方形、两个三角形和两个菱形)。
[中断]
等角多边形证明
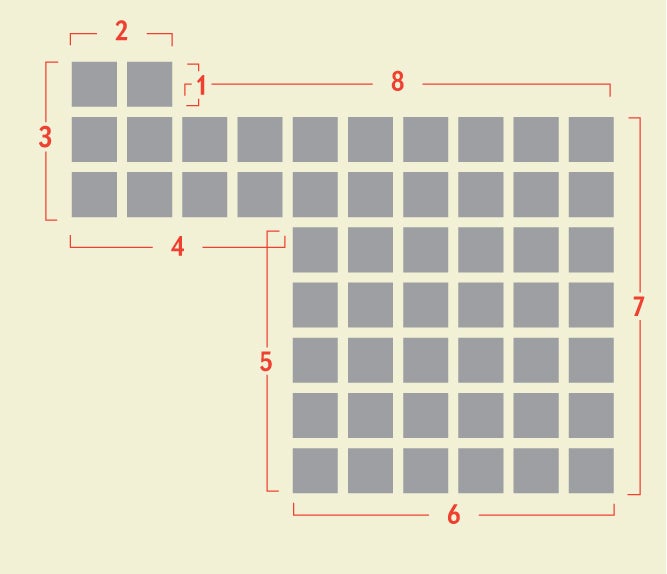
考虑一类称为序列等角多边形的Polygon。所有相邻边都以 90 度角相交,并且边长递增:1、2、3、4,依此类推。最简单的等角多边形,边长为 1-8,如右图所示。这是已知唯一可以平铺平面的序列等角多边形。但是还有更多的等角多边形。你能证明它们的边数必须始终是 8 的倍数吗?
[答案:] 任务是证明对于任何 90 度序列等角多边形,边数必须是 8 的倍数。
将等角多边形想象成一条闭合路径,在标准方格纸的格线上绘制。假设路径从向东的单位移动开始;向东或向北移动为正,向南或向西移动为负。您可以通过在移动序列中每个数字前面加上加号或减号来描述这样的路径,以指示移动方向。例如,谜题样本中显示的 8 边等角多边形具有以下公式: +1 + 2 – 3 – 4 – 5 – 6 + 7 + 8。
因为路径必须闭合才能形成等角多边形,所以所有水平移动(奇数)的总和必须为零,并且所有数字的总和也为零。同样因为路径是闭合的,我们知道边数必须是 4 的倍数,比如 4k。(很容易看出它永远不可能是 4 本身——马丁·加德纳开玩笑说这是一个“四边形结论”。)那么南北移动是偶数长度的移动,2、4、… 4k。因此,南北总距离为 2(1 + 2 + … + 2k) = 2k(2k + 1)。其中一半,k(2k + 1),必须向北,一半向南。
但是如果 k 是奇数,则此距离是奇数,并且不能是偶数长度移动的总和。例如,考虑一个 12 边的等角多边形(在这种情况下,k = 3)。其公式中的偶数(2、4、6、8、10、12)加起来为 42。如果该公式描述了一条闭合路径,则该序列中正数的总和必须等于 42/2 = 21。但是,没有一组偶数可以加起来为 21。因此,无法构造公式来描述 12 边的等角多边形。
这个例子表明,如果边数是 4 的倍数但不是 8 的倍数(k 为奇数的所有情况,例如 12,路径的最后一段是垂直的,无法返回到穿过路径原点的水平格线:向北的正线段之和不能等于向南的负线段的绝对值之和。路径终点将始终在零水平线上方或下方偶数个单位处结束。
[中断]
不受攻击的皇后
国际象棋棋子的属性在许多挑战中发挥作用,包括在一组关于不受攻击的皇后的问题中。想象一下在一个 5 × 5 的棋盘上有三个白皇后和五个黑皇后。你能安排它们,使一种颜色的皇后不能攻击另一种颜色的皇后吗?只有一个解决方案,不包括反射和旋转。
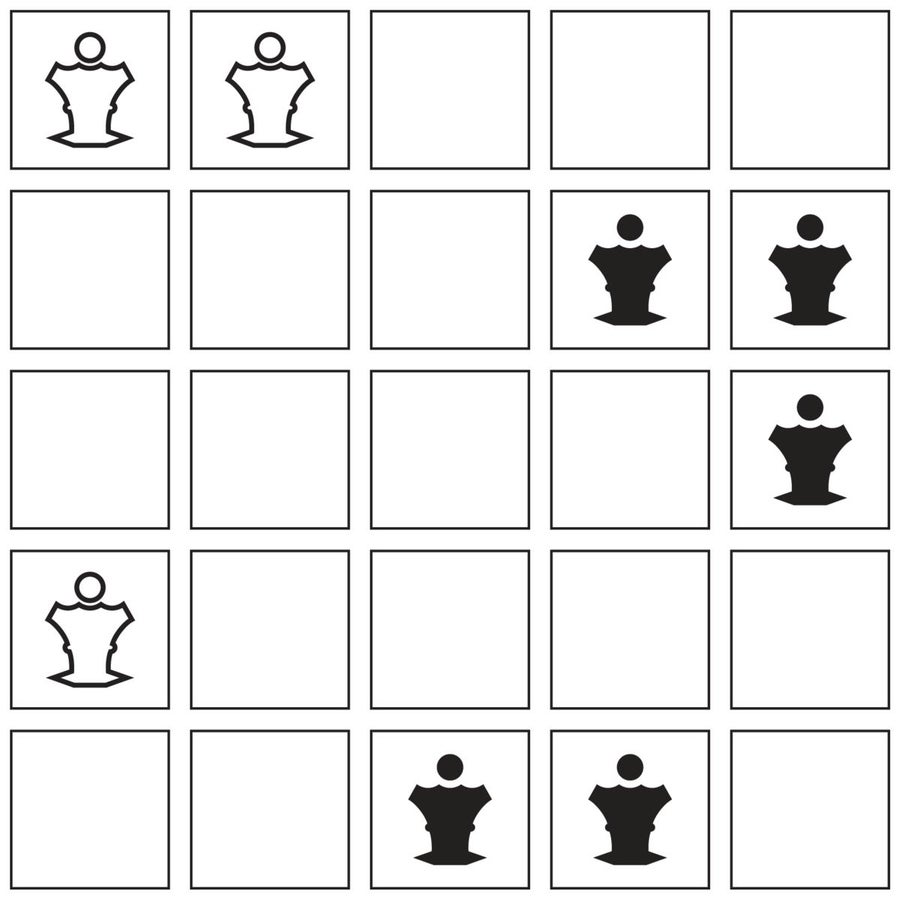
[答案:]