2015年10月,我在瓦努阿图维拉港一所法国高中培训数学教师的时间即将结束。校长邀请我分享卡瓦酒,这是该国的一种传统饮品。正如瓦努阿图的每位社会科学家所发现的那样,分享卡瓦酒是学习的绝佳机会。这种饮料是用同名树木的根制成的,可以使饮用者放松身心,畅所欲言。
第一次接触卡瓦酒也是我接触沙画的开始。那天晚上,一位学员拿出一块铺满细沙的大板子。在仔细地将表面弄平后,他画了一个水平和垂直线的网格。然后,他开始在沙子上描绘沟壑,手指从不抬起。艺术家完成后,他用比斯拉马语解释说:“Hemia hem i wan fis i ronwe i stap unda ston from i kat wan sak,” 意思是“这是一条躲在石头下以躲避鲨鱼的鱼。”
线条的流畅性,加上卡瓦酒的作用,使我陷入了惊奇的状态。这项技术让我想起了用一笔画出复杂图形的经典挑战,笔不能抬起,也不能在同一条线上重复走两次。它也使我想起了数学中的“欧拉图”,它涉及一条遍历每条边恰好一次,并在同一点开始和结束的路径。
支持科学新闻事业
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻事业 订阅。通过购买订阅,您将帮助确保有关塑造我们当今世界的发现和思想的有影响力的故事的未来。
当我思考这些想法时,一位实习生走近我,低语道:“老师,这幅画中的数学在哪里?” 尽管他不可能知道,但这句话将塑造我未来六年的生活,包括我关于沙画的博士研究。一个问题尤其启发了我:这些图画是如何创作出来的?

沙画是用单指笔画绘制的复杂图形。 来源:阿尔班·达·席尔瓦
我的调查比我能想象的还要深入。通过观察沙画专家,了解他们的方法,收集图画和历史,以及探索20世纪民族学家的工作,我开发了一个沙画的数学模型。我的工作表明,这些艺术品可以被建模为算法和代数性质运算的结果。事实上,数学语言被证明适合描述沙画专家的工作。此外,沙画可以帮助我们理解瓦努阿图社会与其环境之间维持的关系。
一种传统艺术
瓦努阿图是一个群岛国家,人口约31.5万人,分布在83个岛屿上。该国是世界上语言密度最高的国家,拥有138种本土语言。学校教授的两种官方语言是法语和英语。比斯拉马语,或比奇拉马语,一种在瓦努阿图使用的英-美拉尼西亚混合语,是通用语言。
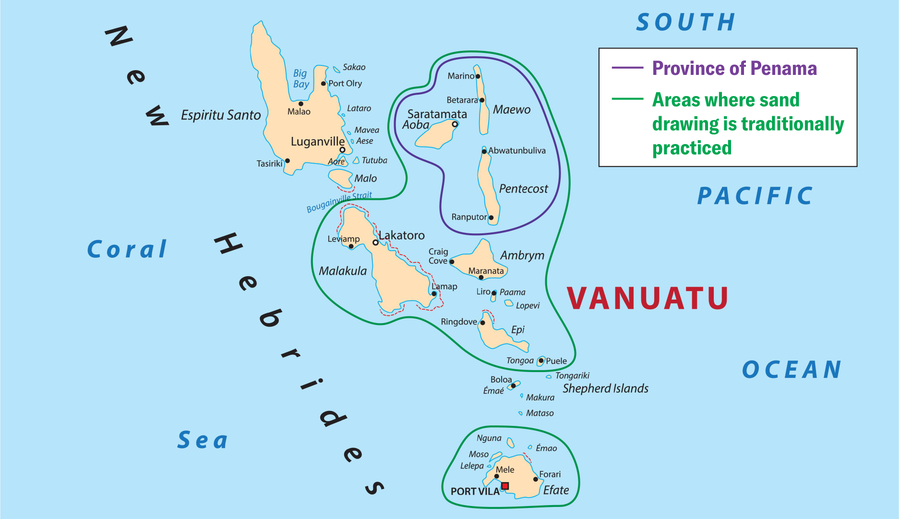
地图显示了瓦努阿图群岛国家的一部分。民族数学家阿尔班·达·席尔瓦研究了该国佩纳马省的沙画,特别是在马埃沃岛和彭特科斯特岛上。来源:Rainer Lesniewski/Alamy Stock Vector (地图); Amanda Montañez (绿色和紫色轮廓及图例)
该国北部和南部的文化各不相同,即使在同一个岛屿内也是如此。例如,沙画习俗仅在一些中部岛屿广泛流传。虽然这种传统让人想起印度泰米尔纳德邦在泥土上所作的绘画,但在许多方面它是独一无二的。2008年,联合国教科文组织将瓦努阿图的沙画列为人类非物质文化遗产的一部分。
我的研究基于2018年在马埃沃岛和2019年在彭特科斯特岛进行的两次实地调查,特别关注彭特科斯特岛北部拉加地区(发音为“拉-拉”)的人们所作的绘画。这些岛屿与奥巴岛一起构成了佩纳马省,并受共同传统的约束,这极大地促进了我的研究。
“沙画”,或比斯拉马语中称为sandroing,可能已有数千年的历史。传统上,它指的是一个人用手指在夯实的土地、沙滩或灰烬中绘制一条连续的闭合线。(这里的“连续”和“闭合”与数学中的含义相同:沙画类似于平面上的闭合连续曲线。)这条绘制的线受到线条或点的复合网格的约束。网格可以是矩形或圆形。
虽然很难知道有多少种设计在使用,但很明显,随着时间的推移,新的设计会出现,而另一些则会消失。一个非常接近知识产权的系统保护着这些图画,使得有时难以敏感地获取这种传统知识,并且具有挑战性。
这些艺术品在其意义上是多维的。一些具有代表性的动物、昆虫或植物图画与这些社会的信仰、宇宙起源、社会组织甚至传统密切相关——这些传统被统称为卡斯托姆。这些图画也可以支持叙事;它们揭示了瓦努阿图中部社会的伦理或政治层面。在许多情况下,每种设计都有一个与这些不同方面相关的本土名称。

一幅沙画描绘了一条鱼躲在石头下以躲避捕食者。 来源:阿尔班·达·席尔瓦
今天,这些社会将这种习俗视为一种传统的图形艺术,有助于人们回忆起仪式、宗教和环境知识。此外,我在拉加地区遇到的一位酋长杰夫·托达利向我解释说,艺术家是代言人:“在图图拉尼[白人外国人]到来之前,彭特科斯特北部的人们不知道如何说话。他们通过手指在地上描绘的图画来表达自己。不是人在说话,而是岩石、石头、山丘和山谷的地面、风、雨、海水在说话。但现在情况颠倒了。是人在说话,而大地、风、雨和大海沉默了。现在[拉加地区的人们]有时会说,‘我们必须为土地说话,因为它不能再为自己说话了。’”
最后,这种短暂的艺术——每幅画一旦完成就会被擦除——激发了讲故事。从业者通常会将他们的图画与故事讲述结合起来,而最有天赋的人能够在绘画的同时做到这一点。他们通过添加与他们的历史相关的细节,包括熟悉的地方、人物、动物甚至蔬菜,来吸引观众的想象力,这并不罕见。
专家和规则
存在不同的专业知识和实践水平。有些人根本不练习沙画。另一些人则知道一些相当简单的图画。“专家”——由他们社会的其他人指定——拥有令人印象深刻的曲目(根据一些人的说法,多达400幅图画)。虽然最早关于沙画的民族志提到这种艺术是男性专属的,但今天情况并非如此。我遇到的一些女性拥有很高的专业水平。
从初学者到专家,每个人都遵循一套“规则”。由于这些社群具有口头传统,因此没有书面记录,但在我的实地调查期间,我列出了一份在大多数情况下都遵循的原则清单。所有图画都从一个网格开始,该网格提供支持并定义一组节点或交叉点和线条。
一个动画展示了经典的龟形沙画设计。 来源:阿尔班·达·席尔瓦
然后,规则指示允许的移动。更准确地说,艺术家必须 (1) 从一个节点移动到另一个节点,而不会穿过相同的路径或在节点以外的地方切割网格,并且 (2) 必须在不抬起手指的情况下返回起点。
我在实地发现了一条额外的规则,事实证明这条规则对我的模型至关重要,如下所述。
玛西亚·阿舍的直觉
我不是第一个认识到这些规则与数学概念相似的人。事实上,我的论文是美国数学家玛西亚·阿舍在 20 世纪 80 年代进行的工作的延续,玛西亚·阿舍是民族数学的先驱。她认为,在沙画中,与数学家所称的图论,特别是与欧拉图,存在明显的联系。
为了理解阿舍的观点有多么革命性,请考虑在她和她的同代人工作之前,学者们普遍认为只有拥有文字的社会才能真正实践数学。他们将对数学知识的调查限制在文字资料上,而忽略了在不使用书面语言的口头传统社会中看到的许多其他实践。
但自从民族数学出现以来,一些学者已经开始推翻这些假设。这种转变无疑始于 20 世纪 40 年代,当时数学家安德烈·韦伊在人类学家克劳德·列维-斯特劳斯的著作《亲属关系的基本结构》中一篇现在著名的附录中证明,澳大利亚 Yolngu 人的亲属关系规则遵循所谓的非平凡群定律。从那时起,研究人员在许多其他地方发现了数学原理,包括马达加斯加的播种游戏和占卜、巴布亚新几内亚特罗布里恩群岛的线绳游戏、安第斯山脉的纺织品和留尼汪岛的装饰性窗帘。
阿舍关于沙画的工作借鉴了一位年轻的民族志学家伯纳德·迪肯的工作,他在 1926 年和 1927 年从瓦努阿图的马莱库拉岛和安布里姆岛收集并转录了 100 多幅沙画。阿舍研究了这些图形,并意识到这些图像可以用数学来描述。
每幅沙画都可以被认为是一个“图”,因为它包含顶点或点,由边或线连接。(图中“图”的定义在数学中是特殊的。在图论中,图是由顶点和边组成的简单图形,用于绘制网络中许多节点的连接——例如,道路连接的城市、互联网连接的计算机,甚至社交关系连接的人。)
阿舍观察到,在沙画中,沙子上描绘的线条可以比作一个图,其顶点包括图案中创建的所有交叉点。边是这些顶点之间的所有弧。这些图也是欧拉图,这意味着沙画艺术家必须只访问每条边一次,并且必须返回起点。阿舍还记录了每个顶点的边数,数学家称之为顶点的“度”。这很重要,因为根据数学家卡尔·希尔霍尔泽创建的欧拉定理,一个连通图是欧拉图,当且仅当每个顶点都具有偶数度。
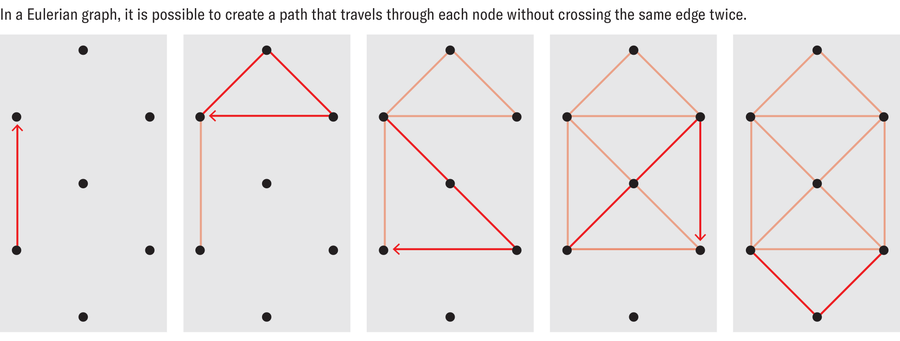
来源:阿尔班·达·席尔瓦/Pour la Science,由阿曼达·蒙塔涅斯重新设计
阿舍从未有机会去瓦努阿图亲眼看看设计师的工作,这无疑限制了她的研究。因此,我自己的研究可以更进一步。阿舍的一个特殊观察结果推动了我对这些图像是如何创建的研究。通过检查迪肯的图画,她观察到其中一些图可以分解为三到四个子步骤,当这些子步骤连接在一起时,就形成了最终的图画。换句话说,每个步骤都产生一个返回起点的子图。当这些子图叠加在一起时,最终的图画就显现出来了。我将这种识别子图的过程称为“分解”。
这些子图为我的工作提出了几个问题:每幅图是否都可能进行这种类型的分解?这些层是如何组合在一起的,顺序重要吗?最重要的是,这些层对沙画艺术家代表什么?
为了进行调查,我首先试图改进阿舍提出的图模型,然后确定计算机是否可以生成沙画的自动分解。阿舍曾提出用一组受变换(例如旋转、平移、对称和反演)影响的模式来建模沙画。但是在听取沙画创作者的意见时,我意识到变换在其设计执行中并没有发挥根本性的作用。事实上,无论图案在网格上的方向如何,他们都使用相同的术语来表示图案。因此,我需要另一种方法来描述这些沙画艺术家的做法。
艺术家本人帮助了我完成这项工作。图对于建模对象(顶点)之间的一组关系(边)非常有用。但在她的工作中,阿舍没有考虑这些关系的性质。通过强调网格的节点、图的顶点和边缘处的曲线,她忽略了艺术家将如何从一个峰值移动到另一个峰值。在询问专家时,我观察到,对于他们来说,运动的方向与节点一样重要:设计师的手指从一个节点移动到另一个节点,从初始方向移动到最终方向,因此节点在被穿过时,根据两条可能的对角线中的一条或另一条,发挥着不同的作用。
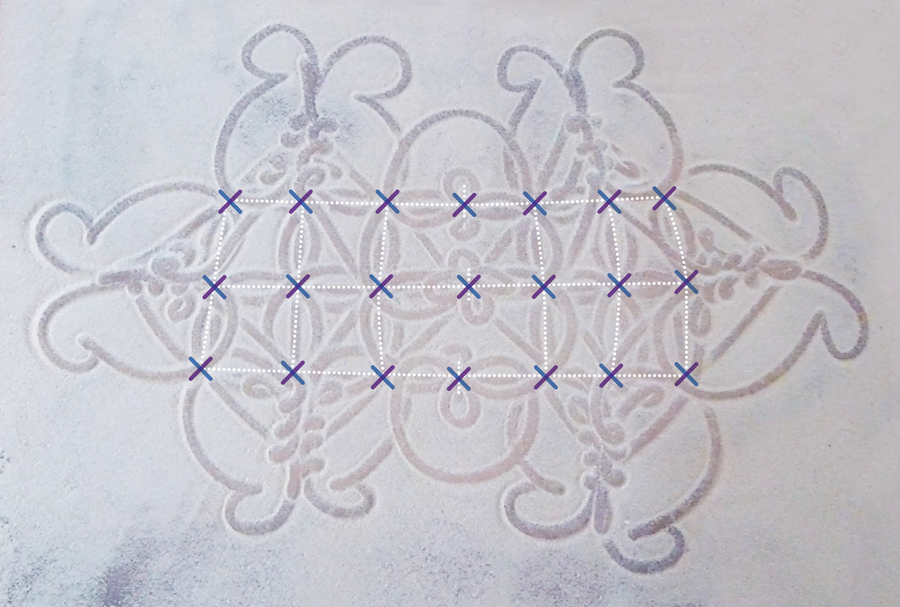
在这幅沙画中的每个节点或交叉点,手指都采用两条对角线路径之一(紫色和蓝色)。 来源:阿尔班·达·席尔瓦/Pour la Science,由阿曼达·蒙塔涅斯重新设计
因此,为了用图来建模沙画设计,可以创建一个图,其中网格的每个节点都被视为两个顶点,而不是一个顶点,每个顶点都被分配给一条对角线。因此,我们获得了一个新的图——命名为 Gmod ——其顶点不是阿舍提出的网格的节点 S ,而是成对的 ( S , d )。
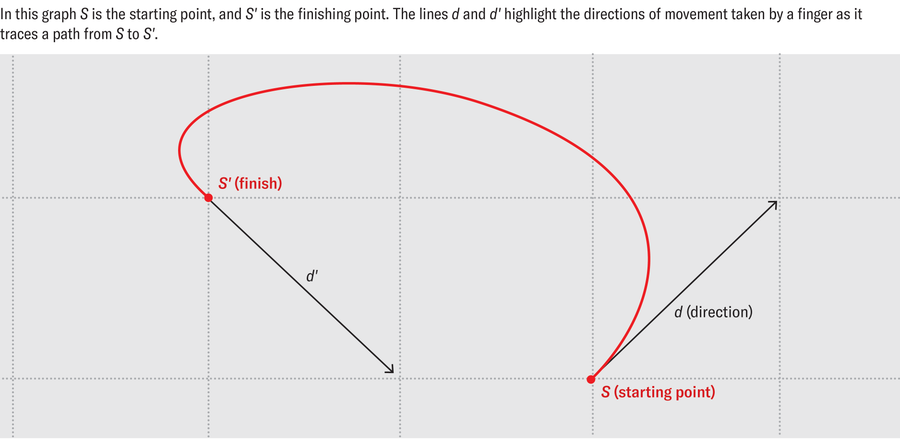
来源:阿尔班·达·席尔瓦,由阿曼达·蒙塔涅斯重新设计
在这个图中, d 是所采取的方向,并且从 S 沿方向 d 出发并在方向 d’ 到达 S’ 的每个绘画动作都对应于顶点 ( S , d ) 和 ( S’ , d’ ) 之间的边。而这个结果 Gmod 图仍然是欧拉图!
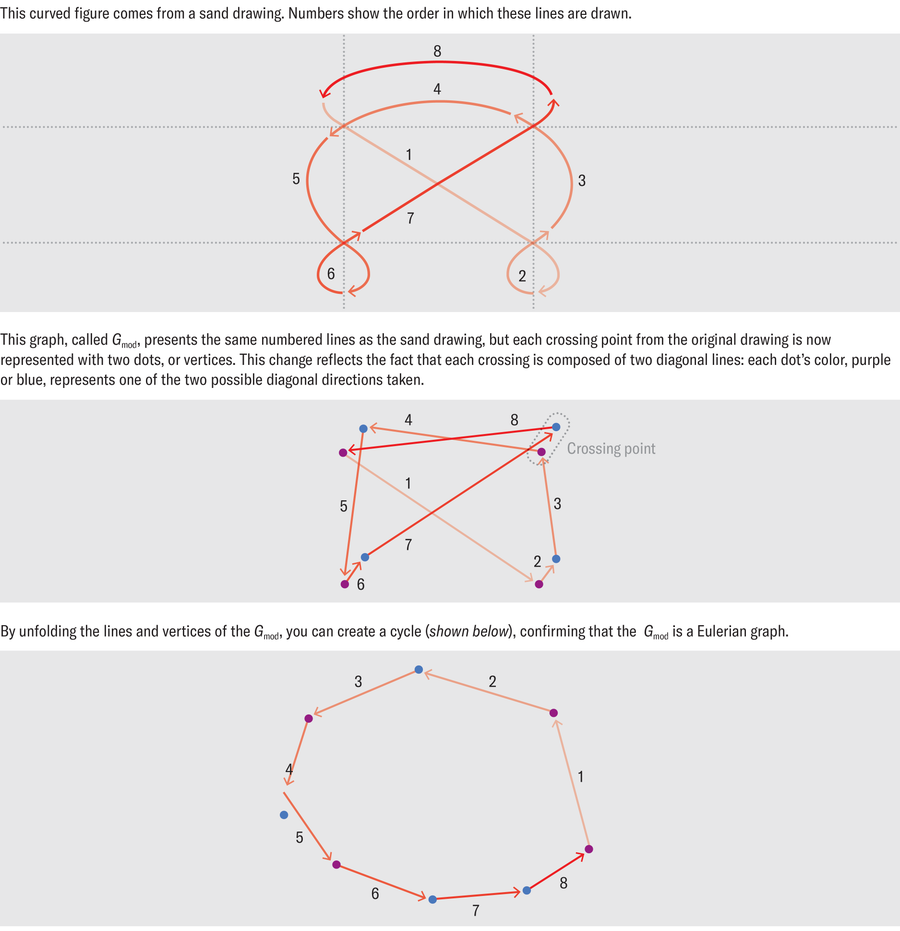
来源:阿尔班·达·席尔瓦,由阿曼达·蒙塔涅斯重新设计
在图画中发现的定理
1912 年,数学家奥斯瓦尔德·维布伦在后来被称为维布伦定理的定理中确定了欧拉图的另一个特征:一个图是欧拉图,当且仅当它可以分解为不相交的环的并集。在图论中,“环”一词指的是一系列不同的连续边,其起点和终点顶点相同。
事实证明,Gmod 图的环对应于沙画的环,因此沙画可以分解为环的不相交并集。
这种方法是否使我们远离了沙画师?我认为不会。相反,环可以为更好地理解他们的方法提供关键。在我收集的 60 幅左右的图画中,我注意到艺术家有时会在完成一个环时暂停绘画。此外,当沙画师被迫寻找另一条路径(比斯拉马语中的 rod )时,他们倾向于重新排列他们在绘画中使用的典型环顺序,或者尝试找到另一种分解为环的方式。
最后,一些环有本土名称,这表明它们对于艺术家来说就像积木一样。事实上,这种对图环的关注似乎也呼应了伴随图画的故事,这些故事在瓦努阿图社会理解世界的方式中发挥着根本性的作用。在我的研究中,我还提出,一些环分解可能与这些社会构想他们与非人类关系的方式有关。
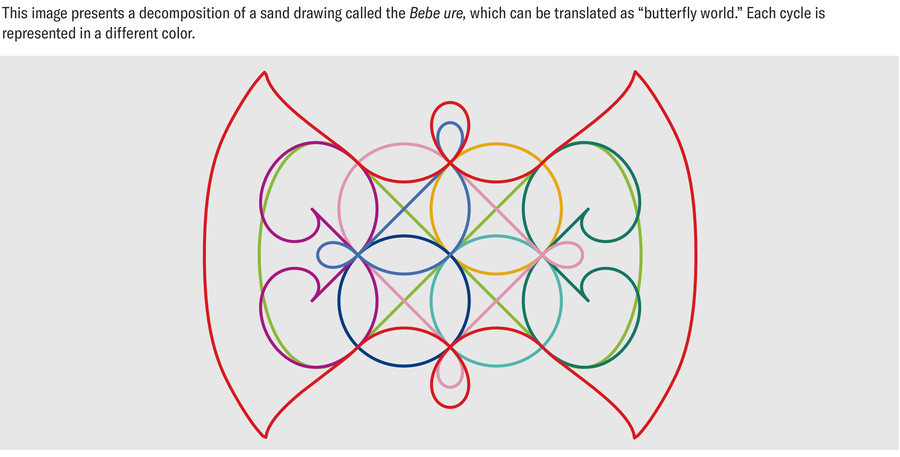
来源:阿尔班·达·席尔瓦
这些结果引发了关于数学的普遍性以及数学在其他文化中采取的形式的问题。它们也为数学教学开辟了前景。自 2010 年以来,获取沙画等传统知识一直是瓦努阿图学校的目标之一,并且是更大的教育去殖民化运动的一部分,就像夏威夷和法国领地新喀里多尼亚的努力一样。然而,在当前的学校课程中,沙画与数学之间没有建立联系。为此,瓦努阿图人皮埃尔·梅桑,新喀里多尼亚大学教育学博士生,正在研究沙画的实践是否可以支持数学教学。我们可以期待他在未来几年从这项调查中学习到的东西。
本文最初发表于 Pour la Science,并经许可转载。
