数字有很多不同的类型,您可能还记得在学校学到的一些:自然数、有理数、无理数、虚数、可计算数和不可计算数。然而,今天,我们将要谈论一些令人愉快的事情,即“快乐数”。是的,它们确实出现在数学中,而且这真的是它们的专业名称。
快乐数没有任何实际应用,但它们确实具有惊人的特性,这就是它们在业余数学家中如此受欢迎的原因。例如,所有自然数都可以分为“快乐”数或“悲伤”数。“快乐”的概括导致了“自恋数”,它们非常专注于自身。
快乐数的概念最初是谁提出的尚不清楚。 它们在 20 世纪 60 年代由英国数学家雷金纳德·艾伦比普及开来:取任意自然数,例如 13,将其数字平方(12 = 1;32 = 9)并将它们相加(1 + 9 = 10)。然后对结果数字重复此快乐计算(12 + 02 = 1)。如果第二次运算的总和为 1,则您已达到“不动点”。也就是说,每次进一步执行相同的过程都将始终产生结果 1。通过重复快乐计算最终产生 1 的数字称为快乐数。
支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
因此,人们不得不称所有其他数字为悲伤数。令人兴奋的是,当您应用快乐计算时,悲伤数也遵循固定的模式。例如,让我们从 4 开始:42 = 16,16 将产生 37(12 = 1 和 62 = 36 的和)。如果我们保持这种模式,我们将得到 16 → 58 → 89 → 145 → 42 → 20 → 4。因为我们从 4 开始快乐计算,所以数字序列重新开始。因此,如果一个数字的重复快乐计算产生值 4、16、37、58、89、145、42 或 20,则该数字注定是悲伤的。艾伦比立即想知道自然数是否都可以分为快乐数(最终结果为 1)或悲伤数(以 4 开头的循环的一部分)——或者快乐计算是否还有其他终点。
有一种快速的方法可以找出答案。为此,您首先需要检查一个数字的平方数字之和可以变得有多大。假设您有一个一位数,例如 9。它的平方 81 大于它本身。对于两位数(例如 99)也是如此:92 + 92 = 162。但是,对于三位数或更多位数的数字,情况并非如此。即使对于 999,其数字平方之和也小于数字本身,即 243。这意味着如果您对一个三位数重复执行快乐计算,您将只会得到三位数值。另一方面,如果您从四位数开始,则第一步的快乐计算将导致三位数结果。
悲伤数算法
要证明每个自然数要么是快乐数,要么是悲伤数,您必须遍历所有三位数。这项任务很繁琐,但并不特别复杂。例如,您可以创建一个简短的算法来辅助以下步骤的过程
1. 为 i、j 和 k 选择一个从 0 到 9 的值。
2. 计算 z = i2 + j2 + k2。
3. 如果 z = 1,则三位数 ijk 是快乐数。
4. 如果 z = 4、16、37、58、89、145、42 或 20,则 ijk 是悲伤数。
5. 如果两种情况都不是真的,则使用“向下取整函数”Floor(x) 设置 i、j 和 k 的新值,该函数将每个十进制数分配给其向下取整的整数值 (Floor(1.6) = 1):i = Floor(z⁄100),j = Floor(a – 100 x i⁄10),k = a – i x 100 – j x 10。使用 i、j 和 k 的这些新值,从步骤 2 继续该算法。
对 i、j 和 k 的所有一位数值重复此算法,结果将始终是快乐数或悲伤数。换句话说,所有三位数要么是快乐数,要么是悲伤数——所有四位数也是如此,因为它们的平方数字之和(快乐计算的第一步)将产生一个三位数。
这个论点可以一直延续到更大的自然数。结果是,每个自然数要么是快乐数,要么是悲伤数。当重复使用快乐计算时,没有哪个值可以逃脱这些命运。
但专家们对这个结果并不满意。例如,数学家们还想知道,快乐数的百分比是多少?它们是否像素数一样随着大小的增加而变得稀有,或者它们是否总是以大致相同的频率出现?
首先,快乐数有无限个。毕竟,10 的每个幂,10x, 都必然对应一个快乐数。
但是它们的密度 ρ 呢,即快乐数与所有自然数的比率?在前 10 个自然数中,有三个快乐数(ρ = 0.3)。在前 100 个中,有 20 个(ρ = 0.2)。在前 1,000 个自然数中,有 143 个快乐数(ρ = 0.143)。甚至在在线整数序列百科全书 (OEIS) 中 也有一个条目专门处理快乐数在 0 到 10n 区间内的频率。因此,如果您计算不同 n 次幂的密度,您将得到以下图片
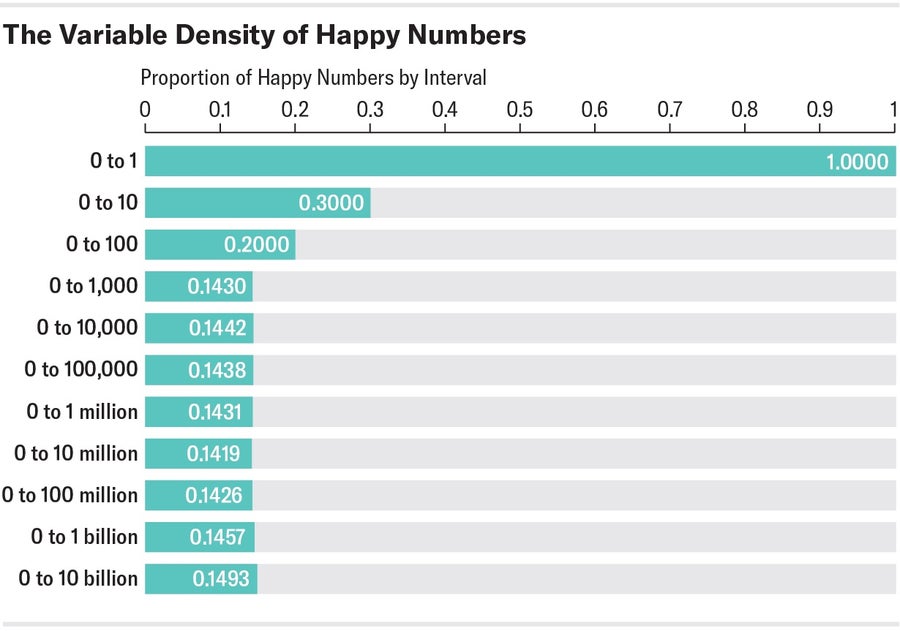
快乐数与给定区间内所有其他数字的比率称为快乐数的密度。 来源: Spektrum der Wissenschaft,由 Amanda Montañez 设计
现在人们可能会假设密度大约等于 14%。 但正如数学家贾斯汀·吉尔默在 2011 年的一篇预印本论文中证明的那样(该论文随后于 2013 年发表),快乐数没有明确定义的密度。他证明,它们的密度取决于所考虑的区间,并且不会收敛到固定极限。 尽管这个结果让很多人感到惊讶,但快乐数远非唯一没有固定、明确密度的数字。
例如,在所有以 1 开头的数字集合中也发现了这种行为。在前九个数字(1、2、3、4、5、6、7、8、9)中,只有一个以 1 开头(数字 1),这对应于 1⁄9 的密度。在前 19 个数字(1、2、...、10、11、12、...、19)中,有 11 个以 1 开头,密度为 11⁄19。在前 99 个数字中,仍然有 11 个以 1 开头,因此在此数字区间内的密度为 11⁄99 = 1⁄9 。在前 199 个数字中,有 110 个以 1 开头,因此密度为 110⁄199,依此类推。
密度在较高值和较低值之间波动,具体取决于您选择的区间。在这种情况下,无法给出整个自然数范围内密度的极限。快乐数也是如此。根据区间,它们的密度在低于 12% 到高于 18% 之间变化。
计算连续快乐数
数学家们关注的另一个问题是:可以有多少个连续的快乐数?前两个是 31 和 32。要找到前三个连续的快乐数,您必须查看四位数的值:1,880、1,881、1,882。
在 2006 年的一篇预印本论文中,数学家郝潘证明 存在任意数量的连续快乐数。(该论文随后于 2008 年发表。)关键是您可能必须搜索很长时间。在 7,839 可以找到一个包含四个连续数字的序列,在 44,488 可以找到一个包含五个数字的序列,在 7,899,999,999,999,959,999,999,996 可以找到一个包含六个数字的序列。
另一个谜题是考虑将快乐数变为 1 需要多少次快乐计算。 这个量可以用来定义一个数的整体快乐程度。迭代次数越少,数字越快乐。因此 1、10、100 等非常快乐,而 13 则略逊一筹。
哪个数是最不快乐但不是悲伤的数?在两位数中,它是 7。从 7 到 1 需要五次迭代。接下来是 356,您需要六次快乐计算才能得到它。
在那之后,事情变得疯狂起来。如果您想要一个更不快乐的数字,您最终会得到一个 977 位数的值:378899999...999。迭代九次的快乐数有 10977 位数——而且从外观上看,迭代次数没有限制。可以为任意数字 n 找到一个快乐数,它仅在重复 n 次快乐计算后才产生 1。因此,不快乐的程度没有限制。
当人们概括快乐数的概念时,事情变得非常令人兴奋。除了对数字平方求和之外,您还可以加上三次方。在这种情况下,自然数不再分为两个阵营,而是分为九个阵营。迭代要么在 1 处结束(“快乐立方体”),要么在其他四个不动点之一处结束(153、370、371、407),要么在四个循环之一中结束:55 → 250 → 133 → 55;160 → 217 → 352 → 160;136 → 244 → 136;或 919 → 1,459 → 919。
回归自身的数字
这种概括引出了数论中的另一个概念。当一个数字由 n 位数字组成时,您可以计算其数字的 n 次幂之和。例如,对于 243,结果是:23 + 43 + 33 = 8 + 64 + 27 = 99。对于某些数字,此计算的结果会使其自身回归。例如 153,因为 13 + 53 + 33 = 153。这样的数字称为自恋数。
所有个位数都是自恋数。事实上,自恋数总共只有 89 个:0、1、2、3、4、5、6、7、8、9、153、370、371、407、1,634、8,208、9,474、54,748、92,727、93,084、548,834,...,最大的是 115,132,219,018,763,992,565,095,597,973,971,522,401。
可以证明,通过估算,没有比这更大的自恋数。假设一个数字有 n 位数字。如果所有数字的值都为 9,则数字的 n 次幂之和的最大大小为:n x 9n。但是,当 n 超过一定大小时,此结果始终小于由 n 位数字组成的最小数字 (10n–1)。因此,这样的数字不可能成为自恋数。
过渡发生在 60 位数时:虽然 60 x 960= 1.08 x 1059 并且因此大于 1059,但 61 x 961= 0.99 x 1060 并且小于 1060。对于所有 n > 60 都是如此。因此,不可能存在由超过 60 位数字组成的自恋数。通过遍历从 0 到 60 位数字的所有数字,可以测试它们的自恋性。事实证明,只有 89 个。
由于自恋数的数量有限,因此与快乐数相比,它们持有的未解决问题要少得多。但是这两个类别都非常适合有趣的消遣。
本文最初发表于 Spektrum der Wissenschaft 并经许可转载。
