当我们的孩子还小时,我们花了很多时间一起在厨房里。我们利用这些机会偷偷地教他们关于科学的知识:热和温度、流体流动、密度、粘度、物理变化、化学反应、酸和碱。我们告诉他们这些性质如何结合起来神奇地使蛋糕通过二氧化碳膨胀;我们告诉他们关于酵母和其他有趣的微生物。
我们也谈论数学:重量和测量、面积和体积。披萨是介绍分数的绝佳方式。我们喜欢一起烤饼干,并使用了许多不同的饼干切刀。我们的儿子喜欢恐龙,所以我们有恐龙饼干切刀,还有花、心、星星和动物。当我们使用饼干切刀时,出现了一个有趣的难题:它们在我们切出的每个形状之间留下了空隙。为了用完所有的面团,必须重新擀面。但之后面团会变暖,必须冷藏后才能再次切割。这很耗时。
一定有更有效率的方法来分割面团。
关于支持科学新闻报道
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。通过购买订阅,您正在帮助确保有关塑造我们当今世界的发现和想法的具有影响力的故事的未来。
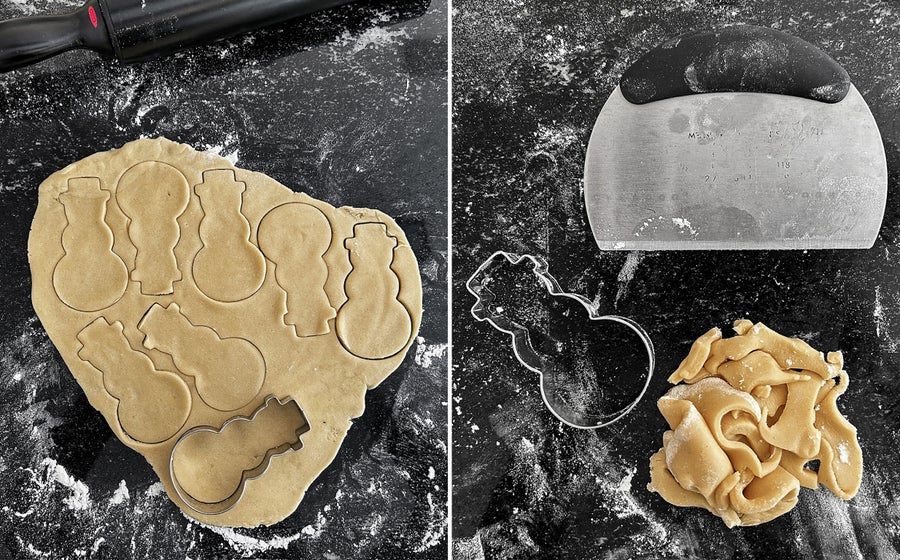
使用更传统的饼干切刀制作饼干通常会留下很多剩余面团。
梅加·萨蒂亚纳拉亚纳
作为一名数学家,我听说过平铺和镶嵌,它们指的是使用一个或多个几何形状覆盖表面,没有重叠和空隙。这就是饼干切刀问题的答案!
所以我寻找镶嵌饼干切刀,但只找到了正方形和六边形。它们有效,但就形状而言,并不是特别有趣。然后,大约 15 年前,第一批 3D 打印机问世了。有可能制作定制饼干切刀,然后就变成了选择形状的问题。许多图形可以用来镶嵌,例如正三角形或不规则三角形、矩形或一些不规则五边形。一些不规则五边形是由已故的业余数学家马乔里·赖斯发现的,可以在Mathemalchemy中看到,这是一个艺术和数学展览,合作者包括杜克大学数学家英格丽·多贝西和纺织艺术家多米尼克·埃尔曼。该展览还展示了一个使用 π 符号的镶嵌饼干切刀,由多贝西进行了适当的调整。
还有其他例子;伊斯兰艺术包括使用五边形对称的美丽而富有创意的设计。
如果我们连接两个或多个图形,那么会有更多选择。例如,八边形和正方形,或五边形和菱形,或 M.C. 埃舍尔的所有惊人作品。但并非所有都适合制作饼干;我们制作了一个埃舍尔蜥蜴形状的饼干切刀,但当我们将图形分开时,腿断了。
所有这些镶嵌都是周期性的,这意味着它们具有重复的图案。在 20 世纪 70 年代,罗杰·彭罗斯发现了两种称为风筝和飞镖的图形,如果遵守一些局部规则(指定飞镖的哪些边可以相互接触),它们只能非周期性地平铺平面(意味着所有可能的配置都是非周期性的)。但如果不遵守规则,那么它们就会周期性地平铺。这非常适合饼干切刀,因为生面团是周期性平铺的,然后饼干可以周期性或非周期性地放置。有关彭罗斯平铺的更多信息,请参见视频频道Veritasium和一个名为“彭罗斯型伊斯兰交错图案”的网页。

镶嵌饼干切刀,例如这种风筝和飞镖形状的切刀,可以创建漂亮的图案,并且比其他形状使用更多的面团。
梅加·萨蒂亚纳拉亚纳
几年前,在我的朋友们的帮助下,我使用 3D 打印机制作了一个风筝和飞镖形状的饼干切刀,它们以周期性方式平铺在一起。烘烤后,这些块可以周期性或非周期性地放置。这效果非常好。
然后,“帽子”出现了。
大约 50 年来,数学家们一直在思考是否可能存在一个可以非周期性地平铺平面的单一图形。在 2023 年,大卫·史密斯、克雷格·卡普兰、柴姆·古德曼-施特劳斯和塞缪尔·迈尔斯设法找到了难以捉摸的非周期性单片平铺,他们称之为“帽子”或“爱因斯坦”。
我的第一个冲动是制作一个帽子形状的饼干切刀。事实证明,在没有空隙或重叠的情况下放置这些块非常困难。但是,发现帽子的人实际上也意识到它可以转化为无限数量的非周期性单片平铺,正如克雷格·卡普兰报道的那样。其中三个单片平铺可以周期性和非周期性地平铺,它们非常适合作为饼干切刀。
史密斯和他的团队称之为“Tile (0,1)”的人字形很容易制作,易于在面团上使用,并且烘烤好的饼干很容易以美丽的图案放置,尤其是在用不同颜色装饰时。另一个完美的候选者是作者称之为“Tile (1,1)”的图形。当与镜像结合时,该图形周期性地平铺,但如果不允许镜像,则仅非周期性地平铺。因此,完美的饼干切刀有两个这样的图形,一个正常,一个反射。
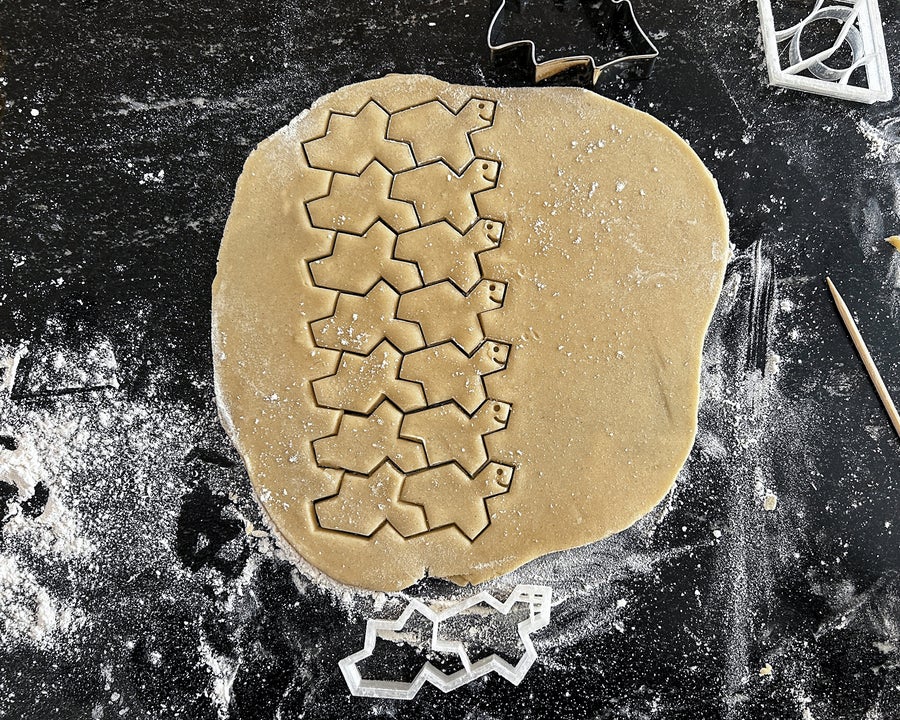
基于大卫·史密斯发现的帽子的饼干切刀可以制作镶嵌图案,从而最大限度地减少面团浪费。
梅加·萨蒂亚纳拉亚纳
史密斯和合作者还发明了一类弯曲的非周期性单片平铺,他们称之为“幽灵”,它也可以变成饼干切刀,最近发现的软细胞也可以。在每种情况下,如果您小心,您可以切割您的饼干面团,最大限度地减少重新擀面和浪费。
当您在节日期间烹饪和烘烤时,如果您能找到一个镶嵌饼干切刀,并且如果您让您的孩子参与进来,您可以利用您本会花费在重新擀面团上的时间来告诉他们关于科学和数学的知识。在我们的例子中,我们的孩子已经长大,但我的镶嵌饼干切刀系列和我都很高兴在我们的孙子孙女到来时分享数学和科学的奇迹。
这是一篇观点和分析文章,作者或作者表达的观点不一定代表《大众科学》的观点。
