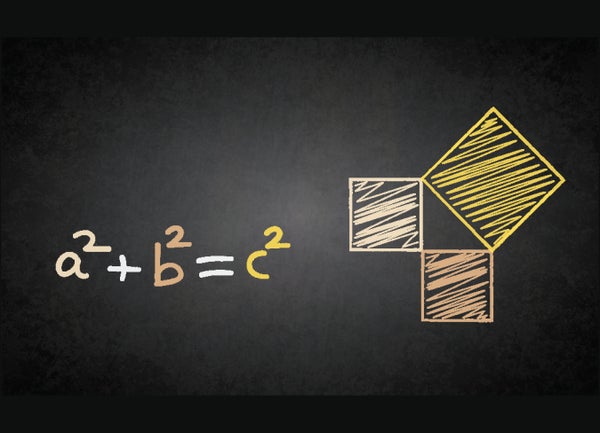两名高中生以一种 20 世纪早期数学家认为不可能的方式证明了勾股定理:使用三角学。
Calcea Johnson 和 Ne’Kiya Jackson 都在新奥尔良的圣玛丽学院就读,她们上个月在美国数学学会的一次会议上宣布了她们的成就。“老实说,这是一种无与伦比的感觉,因为没有什么能与之相比,能够做一些……人们认为年轻人做不到的事情,”约翰逊告诉 WWL-TV,新奥尔良 CBS 分支机构。
如果得到验证,约翰逊和杰克逊的证明将与数学家和教育家伊莱沙·卢米斯相矛盾,后者在他的 1927 年著作勾股定理中指出,勾股定理的任何三角证明都不可能是正确的。 她们的工作与多年来添加到数学档案中的其他一些三角证明相呼应。 每一种方法都避开了“循环逻辑”,从而证明了这个关键定理。 那么,勾股定理的三角证明究竟是什么?为什么卢米斯如此排斥这个想法?
关于支持科学新闻
如果您喜欢这篇文章,请考虑通过以下方式支持我们屡获殊荣的新闻报道 订阅。 通过购买订阅,您正在帮助确保有关当今塑造我们世界的发现和想法的具有影响力的故事的未来。
勾股定理提供了一个方程,通过将其他两条边的平方相加来计算直角三角形的较长边。 它通常表示为 a2 + b2 = c2。 在这个方程中,a、b 和 c 代表直角三角形三条边的长度,直角三角形是指两条边之间有一个 90 度角的三角形。 量 c 是最长边的长度,称为斜边。 虽然该定理以古希腊哲学家毕达哥拉斯的名字命名,但一些历史学家认为早在大约 1000 年前巴比伦就已知道该定理。
德克萨斯农工大学-商业分校的荣誉数学教授斯图尔特·安德森说,该定理“将代数和几何联系起来”。 “语句 a2 + b2 = c2,这是一个代数语句。 但它所来自的图形是一个几何图形。”
与此同时,三角学侧重于取决于角度的函数。 这些函数,如正弦和余弦,是使用直角三角形定义的。 想象一个直角三角形,其中一条边平放在桌子上,另一条边从它与第一条边成直角相交的地方垂直向上。 斜边将在这两条边之间呈对角线延伸。
现在测量斜边和桌子之间的角度。 数学家将这个角的正弦定义为垂直边的高度除以斜边的长度。 这个角的余弦是水平边的长度除以斜边。 因此,勾股定理等价于方程 sin2 x + cos2 x = 1。 “许多基本的三角‘恒等式’只不过是勾股定理,”安德森解释说,他指的是描述不同三角函数之间关系的方程。
卢米斯认为,如果您在勾股定理的证明中使用了这些函数,那么您就从一开始就假设了该定理——这是一个循环论证,因此是一个不可饶恕的数学错误。
但事实并非总是如此。 在他们在美国数学学会会议上的演讲中,杰克逊和约翰逊表示,一种称为正弦定理的三角恒等式不依赖于勾股定理,他们可以用它来证明该定理。
安德森希望杰克逊和约翰逊的证明能够提高学生对数学的兴趣。 “这让我想,如果我还在教课就好了,这样我就可以谈论这件事了,”他说。
过去出现的其他勾股定理的三角证明包括数学家亚历山大·博戈莫尔尼的网站上描述的一些证明。 其中一个证明是由当时的物理学家和本宁顿学院的数学家杰森·津巴撰写的,并于 2009 年发表在Forum Geometricorum上。 该证明使用了一个三角恒等式,该恒等式允许您计算角 x – y 的余弦和正弦,而无需使用勾股定理——如果您知道 x 和 y 本身的余弦和正弦。
2009 年 10 月 26 日,博戈莫尔尼将津巴的证明添加到他的网站,并写道“伊莱沙·卢米斯、我自己以及毫无疑问的许多其他人曾经并且仍然相信,勾股定理的三角证明是不可能的……我很高兴承认自己错了。” 随着时间的推移,博戈莫尔尼在他的网站上添加了更多的三角证明:其中一个证明可以用短短四行字写完。
这个传奇故事表明,即使是最简单的数学也可能让我们感到惊讶。 安德森说:“我认为,数学家们已经学会了不要大胆声称某事是不可能的,因为多年来我们已经为此尴尬了太多次。”
美国数学学会已鼓励新奥尔良的学生提交他们的证明以在同行评审的科学期刊上发表。